本文最后更新于 1159 天前,其中的信息可能已经有所发展或是发生改变。
By SPX
code&concept
# 去除了单位的影响,是无量纲统计量,用百分号表示。在实际应用中可以消除由于不同计量单位/不同平均水平所产生的影响。
# 中心极限定理:
# 无论总体分布如何,只要当抽取的样本容量足够大,那么样本均值的抽样分布就近似于正态分布。
# 点估计及特征
# 直接以样本统计量作为待估计的总体参数的估计值,就是点估计;
# 点估计最大的好处是简便、具体,最大的问题是无从得知估计的准确程度;
# 因此,除非有特别的需求,一般不使用点估计
# 总结:
# 区间估计是以点估计值为中心构造一个区间,同时对该区间是否包含了待估计的总体参数做概率判断;
# 其他条件不变的情况下,要求的置信度越高,区间就越大、估计精度越低;
# 我们要在置信度和估计精度中做平衡选择,通常将置信度定为95%。
# 1.数据描述性分析_集中趋势统计量
# 均值、众数、中位数、百分位数
mean(x,trim=0,na.rm=FALSE); #trim(0,0.5)去掉异常值的比例
sort(x,na.last=NA,decreasing=FALSE,index.return=FALSE)
median(x)
quantile(x,probs = seq(0,1,0.25)) # probs = seq(0,1,0.2)
# 2.数据描述性分析_分散程度的度量
# 方差(var)、标准差(sd)、极差(R)、四分位极差(R1)、变异系数(cv)和标准误(Sm)
# 极差:描述样本分散性的数字特征。当数据越分散时,其极差越大
# 3.数据描述性分析_分布形状的度量
# 偏度系数是刻划数据的对称性指标。关于均值对称的数据其偏度系数为0,右侧更分散的数据偏度系数为正,左侧更分散为负。
# ① Skewness = 0 ,分布形态与正态分布偏度相同。
# ② Skewness > 0 ,正偏差数值较大,为正偏或右偏。长尾巴拖在右边,数据右端有较多的极端值。
# ③ Skewness < 0 ,负偏差数值较大,为负偏或左偏。长尾巴拖在左边,数据左端有较多的极端值。
# 数值的绝对值越大,表明数据分布越不对称,偏斜程度大。
# 峰度系数是描述某变量所有取值分布形态陡缓程度的统计量,简单来说就是数据分布顶的尖锐程度。峰度是四阶标准矩计算出来的。
# ① Kurtosis=0 与正态分布的陡缓程度相同。
# ② Kurtosis>0 比正态分布的高峰更加陡峭——尖顶峰
# ③ Kurtosis<0 比正态分布的高峰来得平台——平顶峰
data_outline <- function(x){
n <- length(x)
m <- mean(x)
v <- var(x)
s <- sd(x)
me <- median(x)
cv <- 100*s/m
css <- sum((x-m)^2)
uss <- sum(x^2)
R <- max(x)-min(x)
R1 <- quantile(x,3/4)-quantile(x,1/4)
sm <- s/sqrt(n)
g1 <- n/((n-1)*(n-2))*sum((x-m)^3)/s^3
g2 <- ((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)^4)/s^4
-(3*(n-1)^2)/((n-2)*(n-3)))
data.frame(N=n, Mean=m, Var=v, std_dev=s,
Median=me, std_mean=sm, CV=cv, CSS=css, USS=uss,
R=R, R1=R1, Skewness=g1, Kurtosis=g2, row.names=1)
}
# 补充函数
apply(x,1,function)
# 1_row;2_col
# 4. 分布函数
dnorm(x, mean=0, sd=1, log = FALSE)
pnorm(q, mean=0, sd=1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean=0, sd=1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean=0, sd=1)
# dnorm是返回正态分布的概率密度函数;
# pnorm是返回正态分布的分布函数;
# qnorm是返回正态分布函数给定概率p后的下分为点;
# rnorm返回由n个正态分布随机数构成的向量;
#5. boxplot绘图
hist(x,freq=F,break=100)
curve(dnorm(x,mean(b,na.rm=TRUE),sd(b,na.rm=TRUE)), xlim=c(x1,x2), col="blue", lwd=3, add=TRUE)
boxplot(A, B, notch=T, names=c('A', 'B'), col=c(2,3))
boxplot(count ~ spray, data = InsectSprays,col = "lightgray")
# 6. 假设检验
# Shapiro-Wilk: 正态分布检验
shapiro.test(x)
# ks.test
# (1). single data
ks.test(x,“pnorm”,mean(x) , sd(x)) #pbinom,pf,pexp
# (2). double datas
ks.test(x,y)
# Pearson
# (1) single data
sort(groupT)
# [1] -5.6 -1.6 -1.4 -0.7 -0.5 0.4 0.7 1.7 2.0
# [10] 2.5 2.5 2.8 3.0 3.5 4.0 4.5 4.6 5.8
# [19] 6.0 7.1
x_groupT<-table(cut(groupT,br=seq(-6,9,by=3)))
p_groupT<-pnorm(seq(-6,9,by=3),mean(groupT),sd(groupT))
p_groupT<-c(p_groupT[1],p_groupT[2]-p_groupT[1],p_groupT[3]-p_groupT[2],p_groupT[4]-p_groupT[3],1-p_groupT[4])
chisq.test(x_groupT,p=p_groupT)
# (2) list data
# H0: x , y 不独立 H1:x , y 独立
x<-c(60, 3, 32, 11)
dim(x)<-c(2,2)
chisq.test(x,correct = FALSE)
# Fisher test(只适用2X2列表)
fisher.test(x)
# McNemar test
# H0: There was no difference in frequency between the two studies in this population
X<-c(49, 21, 25, 107); dim(X)<-c(2,2)
mcnemar.test(X,correct=FALSE)
# Hypothesis testing of binomial distribution populations
binom.test(x,n,p=0.85)
# 符号检验
# H0:Median > Median0
# (1) single data
binom.test(sum(X>99), length(X), al="l")
# (2) double datas
binom.test(sum(x<y), length(x))
# Wilcoxon test
wilcox.test(X, mu=140, alternative="less",exact=FALSE, correct=FALSE, conf.int=TRUE)
wilcox.test(x-y, alternative = "greater")
wilcox.test(x,y,alternative="less",exact=FALSE,correct=FALSE)
# normal population mean and variance tests
# 1. t.test() mu——yuanjiashe
t.test(x, y = NULL,alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,conf.level = 0.95)
t.test(X, Y, var.equal=TRUE, alternative = "less")
t.test(X-Y, alternative = "less")
# 2. var.test()
var.test(x, y, ratio = 1,alternative = c("two.sided", "less", "greater"),
conf.level = 0.95, ...)
#########################################################
# 回归分析(一元线性回归)
# 基本步骤:
# 1. 绘制散点图,观察数据分布情况
plot(dataframe$X,dataframe$Y)
# 2. 构建模型,并查看模型显著性
lm.model <- lm(Y~X+I(X1^2),data=dataframe)
# 补充:回归系数区间估计
beta.int<-function(fm,alpha=0.05)
{
A<-summary(fm)$coefficients
df<-fm$df.residual
left<-A[,1]-A[,2]*qt(1-alpha/2, df)
right<-A[,1]+A[,2]*qt(1-alpha/2, df)
rowname<-dimnames(A)[[1]]
colname<-c("Estimate", "Left", "Right")
matrix(c(A[,1], left, right), ncol=3,
dimnames = list(rowname, colname ))
}
summary(lm.model)
# 3. 若模型显著性较高,将直线方程绘制在散点图上
abline(lm.model)
# 4. 残差分析
y.res <- residuals(lm.model);plot(y.res)
# 异常值标出
text(x,y.res,label=x,adj=1.2)#x表示第x个异常点
# 提取模型信息的函数:
#(1)方差分析
anova(lm.model)
#(2)提取模型公式
formula(lm.model)
# 5. 预测
new_value <- data.frame(x=x0)
lm.predict <- predict(lm.model,new_value,interval="prediction",level=0.95)
# 注意:一定是数据框的格式,返回预测置信区间
# 多元线性回归
# 之前的步骤几乎类似,不同的是可能需要修正拟合模型
new.model <- update(old.model,new.model)
lm.model2 <- undate(lm.model,sqrt(.)~.+x6)
# 5. 逐步优化
# 通过AIC信息统计量,来达到删除或者增加变量的目的,AIC越小越好
step(lm.model)
# Start: AIC= 26.94
# Y ~ X1 + X2 + X3 + X4
# Df Sum of Sq RSS AIC
# - X3 1 0.109 47.973 24.974
# - X4 1 0.247 48.111 25.011
# 6.回归诊断
# 对残差做正态性检验
y.res <- residuals(lm.model)
shapiro.test(y.res)
# 7. 绘制残差图
y.res<-resid(lm.model); y.fit<-predict(lm.model)
plot(y.res~y.fit)
y.rst<-rstandard(lm.model)
plot(y.rst~y.fit)
abline(0.1,0.5);abline(-0.1,-0.5)
# 残差QQ图
plot(lm.model,2)
# 8.影响分析
Reg_Diag<-function(fm){
n<-nrow(fm$model); df<-fm$df.residual
p<-n-df-1; s<-rep(" ", n);
res<-residuals(fm); s1<-s; s1[abs(res)==max(abs(res))]<-"*"
sta<-rstandard(fm); s2<-s; s2[abs(sta)>2]<-"*"
stu<-rstudent(fm); s3<-s; s3[abs(sta)>2]<-"*"
h<-hatvalues(fm); s4<-s; s4[h>2*(p+1)/n]<-"*"
d<-dffits(fm); s5<-s; s5[abs(d)>2*sqrt((p+1)/n)]<-"*"
c<-cooks.distance(fm); s6<-s; s6[c==max(c)]<-"*"
co<-covratio(fm); abs_co<-abs(co-1)
s7<-s; s7[abs_co==max(abs_co)]<-"*"
data.frame(residual=res, s1, standard=sta, s2,
student=stu, s3, hat_matrix=h, s4,
DFFITS=d, s5,cooks_distance=c, s6,
COVRATIO=co, s7)
}
# 9.多重共线性
XX<-cor(dataframe[2:7])#所有自变量X列
kappa(XX,exact=TRUE)
# k < 100,共线性程度小;100 ≤ k ≤ 1000,多重共线性程度中等;k > 1000,多重共线性大。
############################################################
# 方差分析
# 单因素方差分析(H0:方差无显著差异)
dataframe <- data.frame(
X=c(1600, 1610, 1650, 1680, 1700, 1700, 1780, 1500, 1640,
1400, 1700, 1750, 1640, 1550, 1600, 1620, 1640, 1600,
1740, 1800, 1510, 1520, 1530, 1570, 1640, 1600),
A=factor(c(rep(1,7),rep(2,5), rep(3,8), rep(4,6)))
)
dataframe.avo <- aov(X,A,data=dataframe)
summary(dataframe.avo)
# 1.绘制箱型图
plot(dataframe$X,dataframe$A)
# 2. 均值多重比较
pairwise.t.test(X,A,p.adjust.method="none")
# 3. 方差齐次性检验
#(1)误差的正态性检验
attach(dataframe)
shapiro.test(X[A==1])
shapiro.test(X[A==2])
shapiro.test(X[A==3])
shapiro.test(X[A==4])
#(2)方差齐次性检验
bartlett.test(X~A, data=dataframe)
# 4.KW秩和检验(H0:无显著差异)
kruskal.test(X~A, data=dataframe)
kruskal.test(dataframe$X, dataf$A)
# 5.Fiedman秩和检验(H0:无显著差异)
mouse<-data.frame(
x=c(1.00, 1.01, 1.13, 1.14, 1.70, 2.01, 2.23, 2.63,
0.96, 1.23, 1.54, 1.96, 2.94, 3.68, 5.59, 6.96,
2.07, 3.72, 4.50, 4.90, 6.00, 6.84, 8.23, 10.33),
g=gl(3,8),
b=gl(8,1,24))
friedman.test(x~g|b, data=mouse)
# 双因素方差分析
agriculture<-data.frame(
Y=c(325, 292, 316, 317, 310, 318,
310, 320, 318, 330, 370, 365),
A=gl(4,3),
B=gl(3,1,12))
agriculture.aov <- aov(Y ~ A+B, data=agriculture)
summary(agriculture.avo)
# 考虑相互作用
agriculture.aov <- aov(Y ~ A+B+A:B, data=agriculture)
summary(agriculture.avo)
# 方差齐次性检验(同上)
# 不同因素水平重复实验
tree<-data.frame(
Y=c(23, 25, 21, 14, 15, 20, 17, 11, 26, 21,
16, 19, 13, 16, 24, 20, 21, 18, 27, 24,
28, 30, 19, 17, 22, 26, 24, 21, 25, 26,
19, 18, 19, 20, 25, 26, 26, 28, 29, 23,
18, 15, 23, 18, 10, 21, 25, 12, 12, 22,
19, 23, 22, 14, 13, 22, 13, 12, 22, 19),
A=gl(3,20,60),
B=gl(4,5,60))
# 典型相关性分析
cancor(x, y, xcenter = TRUE, ycenter = TRUE)
# example
test<-data.frame(
X1=c(191, 193, 189, 211, 176, 169, 154, 193, 176, 156,
189, 162, 182, 167, 154, 166, 247, 202, 157, 138),
X2=c(36, 38, 35, 38, 31, 34, 34, 36, 37, 33,
37, 35, 36, 34, 33, 33, 46, 37, 32, 33),
X3=c(50, 58, 46, 56, 74, 50, 64, 46, 54, 54,
52, 62, 56, 60, 56, 52, 50, 62, 52, 68),
Y1=c( 5, 12, 13, 8, 15, 17, 14, 6, 4, 15,
2, 12, 4, 6, 17, 13, 1, 12, 11, 2),
Y2=c(162, 101, 155, 101, 200, 120, 215, 70, 60, 225,
110, 105, 101, 125, 251, 210, 50, 210, 230, 110),
Y3=c(60, 101, 58, 38, 40, 38, 105, 31, 25, 73,
60, 37, 42, 40, 250, 115, 50, 120, 80, 43)
)
test<-scale(test)
ca<-cancor(test[,1:3],test[,4:6])
corcoef.test<-function(r, n, p, q, alpha=0.1){
m<-length(r); Q<-rep(0, m); lambda <- 1
for (k in m:1){
lambda<-lambda*(1-r[k]^2);
Q[k]<- -log(lambda)
}
s<-0; i<-m
for (k in 1:m){
Q[k]<- (n-k+1-1/2*(p+q+3)+s)*Q[k]
chi<-1-pchisq(Q[k], (p-k+1)*(q-k+1))
if (chi>alpha){
i<-k-1; break
}
s<-s+1/r[k]^2
}
i
}
# 双因素方法分析
# 1. 分析前先对因素A和B各做正态性检验,使用shapiro.test()
shapiro.test(Y[A==1] ,data=tree)
shapiro.test(Y[B==1] ,data=tree)
# 2. 分析前先对因素A和B做方差齐次性检验,使用bartlett.test()
bartlett.test(Y~A,data=tree)
bartlett.test(Y~B,data=tree)
# 3. 满足正态和方差齐次性,再做双因素方差分析
bartlett.test(Y~A,data=tree)
bartlett.test(Y~B,data=tree)
# 4. 方差分析
summary(aov(Y~A+B+A:B,data=tree))
# 5. 多重检验(1)在以下四个散点图中,其中适用于作线性回归的散点图为(B)
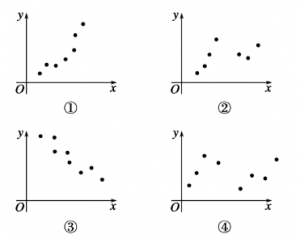
A.①② B. ①③ C. ②③ D. ③④
(2)以下的系统聚类方法中,哪种系统聚类直接利用了离差平方和。(D)
A. 最长距离法
B. 组间平均连接法
C. 组内平均连接法
D. WARD法
(3)Q型聚类法是按样本进行聚类,R型聚类法是按变量进行聚类。
二、简答题(30分=2*15分)
(1)请写出3-4个测度数据离散程度的统计量。
极差、方差、标准差、四分位极差、变异系数、标准误
(2)请写出100个服从二项分布(X~b(5,0.3))随机数的命令。
rbinom(100,5,0.3)
三、操作题(55分)
以小鼠为研究对象研究正常肝核糖核酸(RNA)对癌细胞的生物作用,试验分别对
照组(生理盐水)、水层RNA组和酚层RNA组,分别用此3种不同处理方法诱导
肝癌细胞的果糖二磷酸酯酶(FDP酶)活力,数据如RNA.xls文件所示【评分标准
:每项功能要点的成功实现,分别得10-25分,共55分】
① 根据所给数据信息,确定合适的方法(说明原因)(10分)
② 读入数据,检验3种不同处理的诱导作用是否相同(20分)
③ 根据上述方法计算的P值,画出对应的boxplot(25分)
rat <- data.frame(X = c(2.79, 2.69, 3.11, 3.47, 1.77, 2.44, 2.83, 2.52, 3.83,
3.15, 4.7, 3.97, 2.03, 2.87, 3.65, 5.09, 5.41, 3.47, 4.92, 4.07, 2.18, 3.13,
3.77, 4.26), A = factor(rep(1:3, c(8, 8, 8))))
fit.aov <- aov(X ~ A, data = rat)
summary(fit.aov)
plot(rat$X ~ rat$A)




